Introduction

Suppose a recursive function $T(n)$ is defined as follows: $T(n) = aT(n/b) + f(n)$, where $a \geq 1$ and $b > 1$ are constants and $f(n)$ is a given function. It means we divide the problem into $a$ subproblems, each of size $n/b$, and the cost of dividing and combining the subproblems is $f(n)$.

Theorem

If $T(n) = aT(n/b) + O(n^d)$, then:

$$ T(n)=\left\{ \begin{aligned} &O(n^{log_ba}) & \text{if } a>b^d \\ &O(n^dlog n) & \text{if } a=b^d \\ &O(n^d)& \text{if } a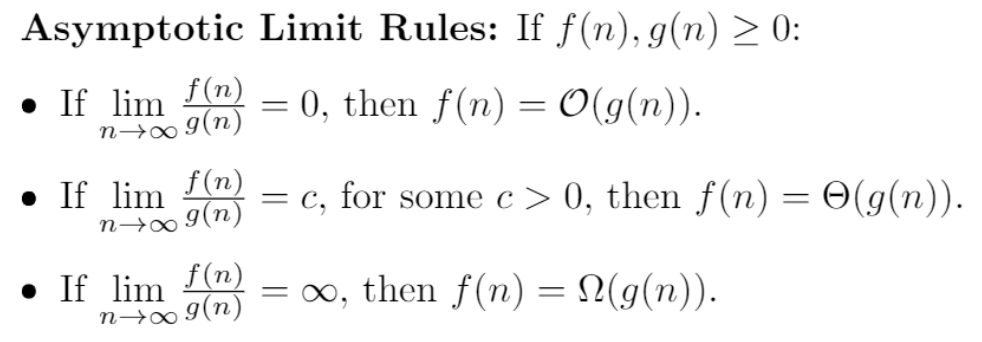Preliminary

Proof

After reconsideration, I found that the initial proof is just kidding. Here is a detailed proof: https://www.luogu.com.cn/article/w3avh1ku

Notation

• $O$: Big O notation, which is used to describe the upper bound of a function. Typically, when $x\rightarrow\infty$, $f(x)\leq M\cdot g(x)$ (M is a constant).
• $\Theta$: Theta notation, which is used to describe the tight bound of a function.
• $\Omega$: Omega notation, which is used to describe the lower bound of a function.

---

We can draw a recursion tree to analyze the time complexity of the recursive function:

Number	Time
1	$f(n)$
$a$	$f(n/b)$
$a^2$	$f(n/b^2)$
$\cdots$	$\cdots$
$a^{log_b n}$	$f(1)$

If $f(n)=n^d$, we get $$\begin{aligned}T(n) =& f(n) + af(\frac{n}{b}) + a^2f(\frac{n}{b^2}) + \cdots + a^{log_b n}f(1)\ =&f(n)(1+\frac{a}{b^d}+\frac{a^2}{b^{2d}}+\cdots+\frac{a^{log_b n}}{b^{dlog_b n}})\end{aligned}$$

Suppose $q=\frac{a}{b^d}$, then $T(n)=f(n)(1+q+q^2+\cdots+q^{log_b n})$. We can use the geometric series formula to simplify the equation: $$T(n)=f(n)\frac{1-q^{log_b n+1}}{1-q}$$

• $q>1$: Noticing that $q^{log_b n}=n^{log_b q}$, so $T(n)\approx f(n)n^{log_b q}=f(n)n^d\Rightarrow T(n)=\Theta(n^d)$.
• $q=1$: $T(n)=f(n)log_b n\Rightarrow T(n)=\Theta(n^dlog n)$.
• $q<1$: $T(n)=f(n)\frac{1-q^{log_b n+1}}{1-q}\leq\frac{f(n)}{1-q}\Rightarrow T(n)=\Theta(f(n))$.

Application

• Large number addition: $T(n)=3T(n/2)+O(n)$ (We can divide each number into two parts and use three registers to calculate the following additions), $a=3$, $b=2$, $f(n)=O(n)$, $a>b^d$, $T(n)=\Theta(n^{log_2 3})$.
• Merge sort: $T(n)=2T(n/2)+O(n)$, $a=2$, $b=2$, $f(n)=O(n)$, $a=b^d$, $T(n)=\Theta(n\log n)$.