Introduction

Suppose a recursive function is defined as follows: , where and are constants and is a given function. It means we divide the problem into subproblems, each of size , and the cost of dividing and combining the subproblems is .

Theorem

If , then:

Preliminary

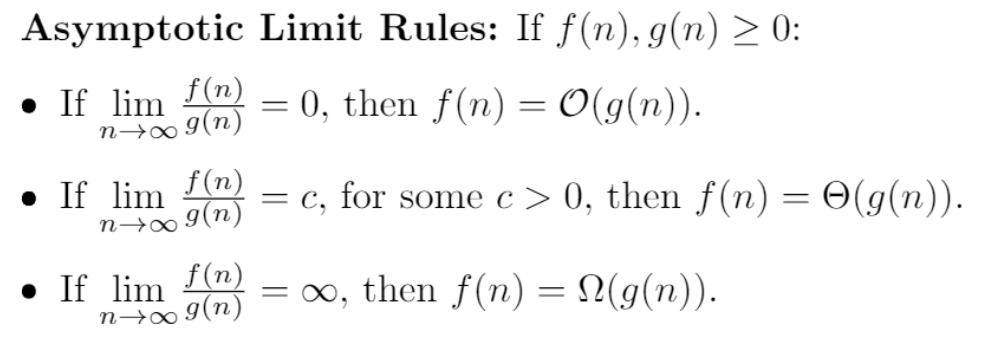
Proof

After reconsideration, I found that the initial proof is just kidding. Here is a detailed proof: https://www.luogu.com.cn/article/w3avh1ku

Notation

• : Big O notation, which is used to describe the upper bound of a function. Typically, when , (M is a constant).
• : Theta notation, which is used to describe the tight bound of a function.
• : Omega notation, which is used to describe the lower bound of a function.

---

We can draw a recursion tree to analyze the time complexity of the recursive function:

Number	Time
1

If , we get

Suppose , then . We can use the geometric series formula to simplify the equation:

• : Noticing that , so .
• : .
• : .

Application

• Large number addition: (We can divide each number into two parts and use three registers to calculate the following additions), , , , , .
• Merge sort: , , , , , .