Content

1. Intro
2. Comparison
3. Terminology
4. Method
   1. Initialization
   2. 3D Gaussians
   3. Rendering
   4. Loss
   5. Optimization

Intro

A new method for real-time radiance field rendering, which generates high-quality new views of a scene from an image set. Applying 3D Gaussian Distribution to present the radiance field realizes the fast training and real-time rendering.

Comparison

Feature	3DGS	NeRF	Mesh
Representation	Gaussian distribution (Hybrid)	Neural field (implicit)	Vertices, edges, faces (explicit)
Rendering Speed	Fast (Real-time)	Slow	Medium
Memory Consumption	Low	High	Low
Detail	Good	Excellent	Moderate
Flexibility	High (Differentiable)	High (Differentiable)	Low (hard for gradient)
Application	Dynamic scenes, real-time applications	Static scenes, high-quality rendering	Simple geometries, traditional graphics

Terminology

• Radiance Field: A function represents the light intensity in 3D space.

  • Inplicit radiance field utilizes neural networks (continous func) to represent the appearance and geometry
  • Explicit radiance field uses discrete data structures (Mesh, point cloud, voxel) directly
  • 3D Gaussian ellipsoid is distributed discretely while continuous in internal space

• Projection&Rasterization:

  1. Projection: Project the 3D Gaussian ellipsoids to the 2D image plane, to specify their positions and sizes.

  2. Rasterization: Transform the 2D Gaussian projection to discrete pixels and calculate the color&transparancy.

Method

Initialization

SfM Motion Structure Recovery:

• Starting from the acquired series of images of the target
• Inference the position of each camera
• Get the feature points in the photos
• Obtain a sparse 3D point cloud in world coordinates as the initial input of 3D Gaussian distribution.

3D Gaussians

Generate 3D Gaussian ellipsoids for each point in the point cloud. All parameters are learnable and optimized by backpropagation.

• Position: (x,y,z)
• Shape: , where is the rotation matrix and is scale matrix.
• Color: Apply forth-order Spherical Harmonics (SH) to represent the rgb color(3*16 parameters).
• Opacity: is the Opacity of the Gaussian ellipsoid.

Rendering

1. Projection: Splatting the 3D Gaussians to 2D image plane.
2. Rasterization: Apply the rendering equation from opacity and color.
   • In NeRF, , where is the accumulated transparancy whether the ray is absorbed, is the density function, representing the intensity that the light is absorbed, and are the near and far distance of the ray.
   • In 3DGS, the color is not obtained from accumulating the point along the ray, while from the Gaussian ellipsoid. And by sorting the depth of the ellipsoids, we use Alpha Blending: , where is the color, is the opacity of the Gaussian ellipsoid (more transparent, more close to 0)

Loss

• L1 Loss:

  Compare the difference in pixel level between the rendered image and the ground truth.

• D-SSIM Loss:

  Compare the structural similarity between the rendered image and the ground truth, including the luminance, contrast, and structure.

SfM sample points, , RGB, will be optimized by backpropagation.

Optimization

1. Pruning: Set the threshold of the opacity, and remove the Gaussian ellipsoids too close to the camera.

2. Adaptive Control of Gaussians:
   

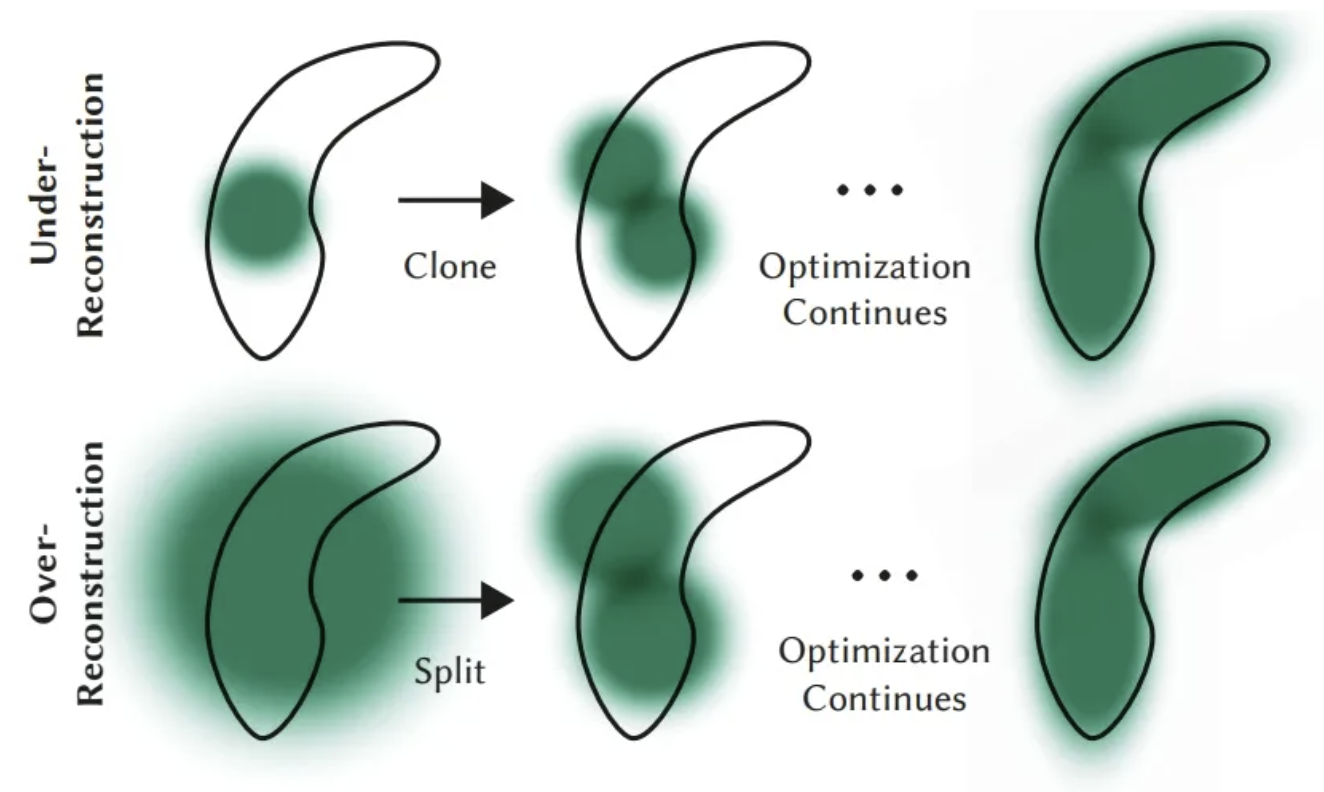
   • Over-reconstruction (gradient is large, too steep): Clone a new Gaussian ellipsoid to cover the space along the position gradient.
   • Under-reconstruction (variance is large, too moderate): Split the Gaussian ellipsoid into two smaller ones around it.
   • By doing this, the newly cloned Gaussian points can better adapt to the geometric features of the scene, fill in areas where details are missing, and thus improve the quality of the reconstruction.

3. Patchification:

   • Split the screen into 16x16 tiles
   • For each tile, only keep the Gaussian projections overlapped with the tile (if covering more than one tiles, copy and tag it to be unique in each tile), which reduces the computation complexity.